Get the Shortest Path in Binary Matrix Using Python

The challenge

In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

• Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
• C_1 is at location (0, 0) (ie. has value grid[0][0])
• C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
• If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right.  If such a path does not exist, return -1.

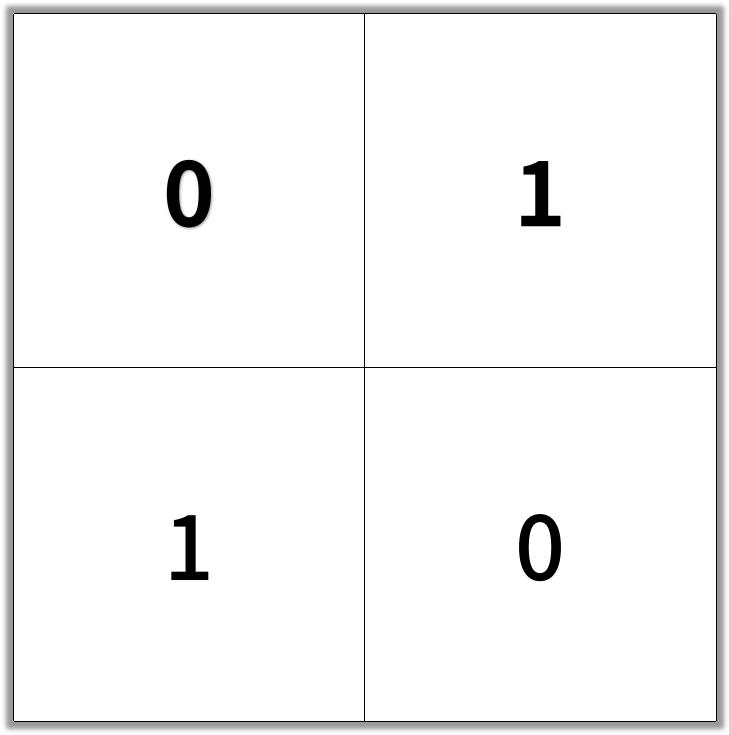
Example 1:

Input:

[[0,1],[1,0]]

Output: 2

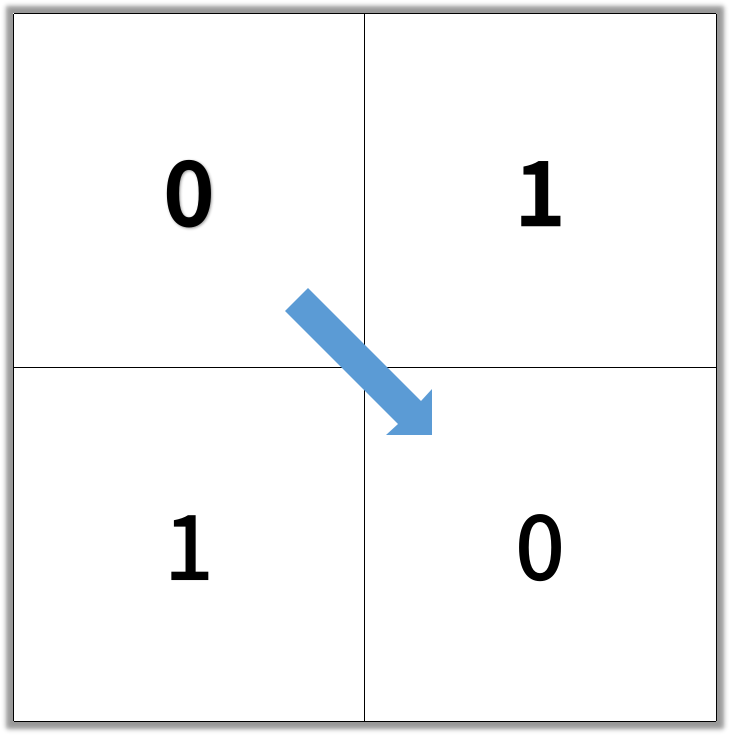
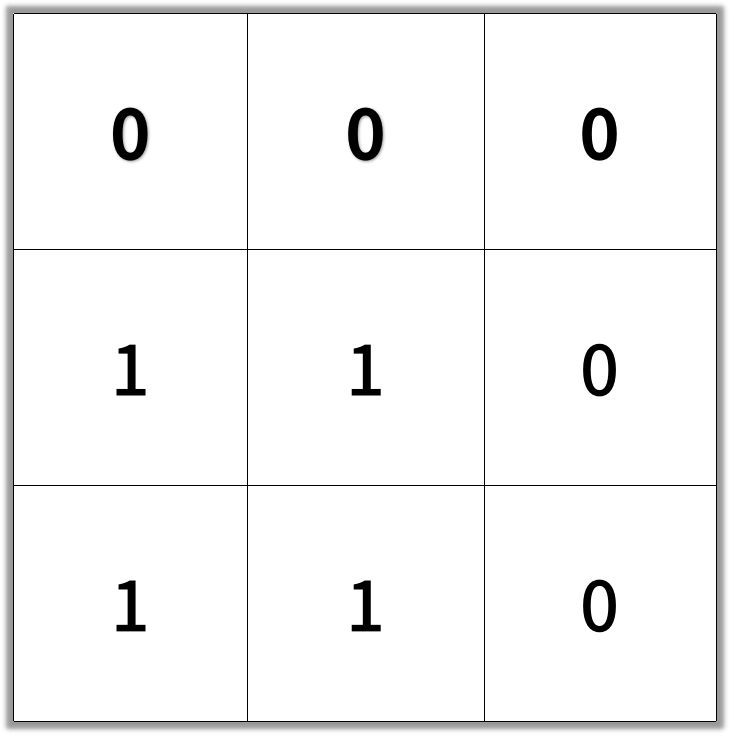
Example 2:

Input:

[[0,0,0],[1,1,0],[1,1,0]]

Output: 4

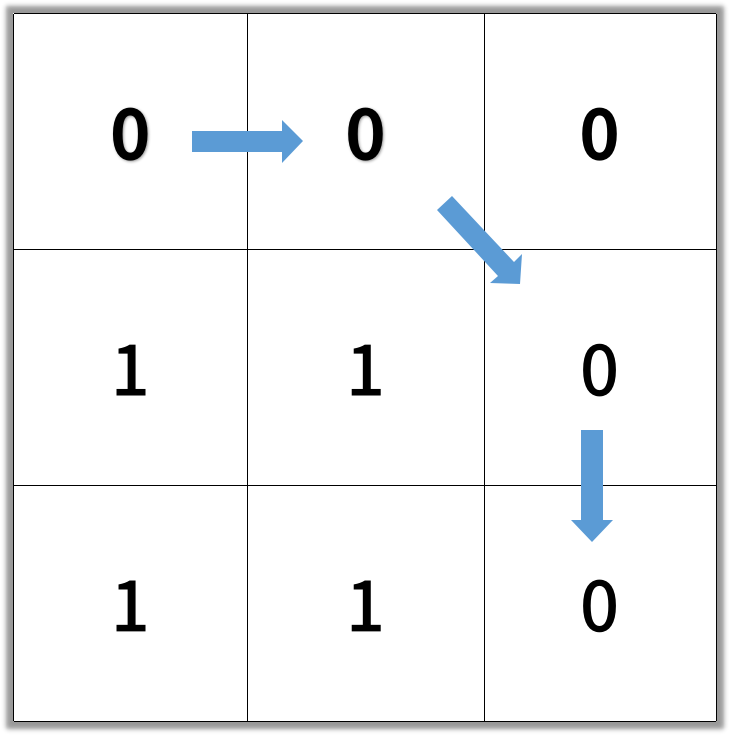
Note:

1. 1 <= grid.length == grid[0].length <= 100
2. grid[r][c] is `` or 1

The solution

def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
    """
    :type grid: List[List[int]]
    :rtype: int
    """

    if grid[0][0] != 0:
        return -1

    q = [[0, 0, 1]]
    grid[0][0] = 1

    while len(q) != 0:
        # print(q)
        k, m, d = q.pop(0)

        # grid[k][m] = 1
        if k == m == len(grid) - 1:
            return d

        # UP
        if k - 1 >= 0 and grid[k - 1][m] == 0:
            q.append([k - 1, m, d + 1])
            grid[k-1][m] = 1

        # DOWN
        if k + 1 < len(grid) and grid[k + 1][m] == 0:
            q.append([k + 1, m, d + 1])
            grid[k+1][m] = 1

        # LEFT
        if m - 1 >= 0 and grid[k][m - 1] == 0:
            q.append([k, m - 1, d + 1])
            grid[k][m-1] = 1

        # RIGHT
        if m + 1 < len(grid[0]) and grid[k][m + 1] == 0:
            q.append([k, m + 1, d + 1])
            grid[k][m+1] = 1

        # TOP LEFT
        if k - 1 >= 0 and m - 1 >= 0 and grid[k - 1][m - 1] == 0:
            q.append([k - 1, m - 1, d + 1])
            grid[k-1][m-1] = 1

        # TOP RIGHT
        if k - 1 >= 0 and m + 1 < len(grid[0]) and grid[k - 1][m + 1] == 0:
            q.append([k - 1, m + 1, d + 1])
            grid[k-1][m+1] = 1

        # BOTTOM LEFT
        if k + 1 < len(grid) and m - 1 >= 0 and grid[k + 1][m - 1] == 0:
            q.append([k + 1, m - 1, d + 1])
            grid[k+1][m-1] = 1

        # BOTTOM RIGHT
        if k + 1 < len(grid) and m + 1 < len(grid[0]) and grid[k + 1][m + 1] == 0:
            q.append([k + 1, m + 1, d + 1])
            grid[k+1][m+1] = 1

    return -1